Mathematische Grundlagen

Grundlage des Naive Bayes Klassifikatoren bildet die Wahrscheinlichkeitstheorie. Folgend werden die allgemeinen Grundlagen beschrieben. Beim einmaligen Werfen eines fairen Würfels sind die möglichen Elementarereignisse des Experiments:

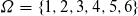
Für jedes Element ω aus der Menge Ω gilt die gleiche Wahrscheinlichkeit.

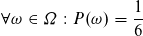
Demnach ist die Summe der Wahrscheinlichkeiten der Elementarereignisse 1.

(Streng mathematisch genommen ist diese Definition für unendlich große Ω nicht korrekt, aber für den Bayes Klassifikator und für dieses Beispiel ist dies irrelevant, da der Wahrscheinlichkeitsraum diskret ist)

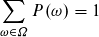
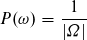
Die Wahrscheinlichkeit eine 6 zu Würfeln ist zufolge 1/6.

Eine Teilmenge A aus Ω wird als Ereignis bezeichnet. Die Wahrscheinlichkeit des Ereignisses A ist die Summe der Wahrscheinlichkeiten aller Elementarereignisse aus A

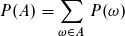
Das Ereignis A könnte z.B. das Würfeln einer geraden Zahl sein.

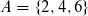Die Wahrscheinlichkeit für das Eintreffen von A beträgt 50%.

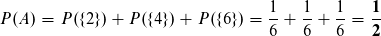
Nun erweitern wir unser Experiement auf das zweifache Werfen eines fairen Würfel.

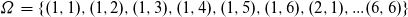
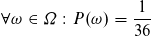
Wir definieren das Ereignis A neu: die summierte Augenzahl beider Wüfel ist 10.

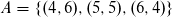
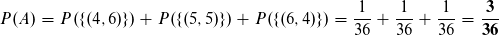
Das Ergebnis B bedeutet, dass der erste Wurf eine 6 ist.

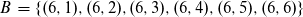
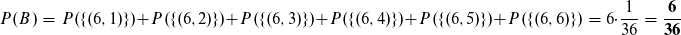
Wenn man die Ereignisse A und B miteinander verknüpft, dann muss der erste Wurf eine 6 sein und die Augenzahl muss 10 betragen.

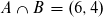
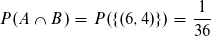
Bedingte Wahrscheinlichkeit

Die bedingte Wahrscheinlichkeit P(A|B) beschreibt, die Wahrscheinlichkeit, dass das Ergebnis A eintritt, unter der Bedingung, dass das Ergebnis B bereits eingetreten ist. In unserem Beispiel bedeutet dies folgendes. Unter der Bedingung, dass die erste Zahl eine 6 ist (Ergebnis B), wie groß ist dann die Wahrscheinlichkeit, dass die Augensumme 10 beträgt (Ergebnis A)?

B ist gegeben:

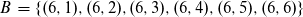
In der Menge B gibt es ein Element, welches auch A entspricht.

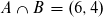Somit beträgt die Wahrscheinlichkeit von A innerhalb B:

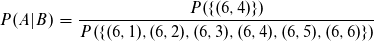
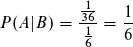
Da für P(A|B) gilt:

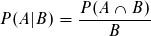
auch bekannt als Bayesches Theorem.

Komplette Definition des Theorems:

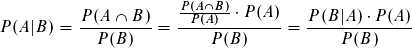
Author: Sven Schirmer