Grundlagen
Definition
Decision Trees werden im Data Mining im allgemeinen verwendet um den Wert einer Zielvariable, basierend auf diversen Input Variablen, zu bestimmen. Decision Trees dienen der darstellung von Entscheidungsregeln. Die hierarchische Darstellung in Baumdiagrammen veranschaulichen aufeinanderfolgende Entscheidungen. [1]
Die Erstellung bzw. das Trainieren eines Decision Trees ist typischerweise ein hierarchisches partitionieren von Trainingsdaten mit hilfe von Entscheidungen. Die Entscheidung an einem Knoten des Decision Trees wird als Split-Kriterium bezeichnet und ist üblicherweise eine Bedingung über ein oder mehrere Input Variablen des Trainings Datensatzes, mit dessen Hilfe der Decision Tree erstellt wird. Das Split-Kriterium teilt den Datensatz in zwei oder mehr Teile. Beispiel: Wenn Alter eine Input Variable ist und das Split-Kriterium Alter ≤ 30, dann enthält der linke Zweig des aktuellen Knotens alle Trainingsdaten für die das Split-Kriterium erfüllt ist, also alle Trainingsdaten in denen die Variable Alter den Wert 30 nicht überschreitet. Alle anderen Daten sind im rechten Zweig vertreten. Die letzten Knoten werden als Blätter bezeichnet und bestimmen den eigentlichen Wert der Zielvariable. Der Wert ist der dominanteste Wert von den verbleibenden Trainingsdaten. Das Erstellen von Knoten, basierend auf Splitkriterien, kann mit Stopp-Kriterien unterbrochen werden um einen zu großen Decision Tree zu vermeiden. Eine weitere Möglichkeit ist das Beschneiden bzw, pruning eines Decision Trees um ein Overfitting zu verhindern. Overfitting bezeichnet im allgemeinen das anlernen von rauschenden bzw. ausreisenden und fehlerhaften Daten. Dies gilt zu vermeiden. [1]
Mithilfe des Trainings Datensatzes wird die Erstellung des Decision Trees, bzw. das Split-Kriterium, überwacht. Somit gehören Decision Trees im Data Mining Bereich zu den Klassifikationsmethoden. [1]
Pseudocode
Der nachfolgende Pseudocode zeigt einen generischen Trainings Algorithmus für das Erstellen eines Decision Trees: [1]
Algorithm GenericDecisionTree(Data Set: D)
begin
Create root node containing D;
repeat
Select an eligible node in the tree;
Split the selected node into two or more nodes
based on a pre-defined split criterion;
until no more eligible nodes for split;
Prune overfitting nodes from tree;
Label each leaf node with its dominant class;
end
Nachdem der Decision Tree erstellt wurde, wird dieser benutzt um eine Zielvariable von einer Input Datenmenge zu bestimmen. Der Decision Tree wird dabei von oben nach unten traversiert bis ein Blattknoten erreicht wird. Die nachfolgende Abbildung illustriert beispielhaft einen Decision Tree.
Decision-Tree für ein Kredit Beispiel. [2]
Splitkriterien
Ein Split-Kriterium sind Bedingungen über ein oder mehrere Input Variablen einer Instanz des Trainings Datensatzes. Splitkriterien werden verwendet um einen Trainingsdatensatz zu partitionieren. Das Ziel ist es, Splitkriterien zu finden, welche den Unterschied zwischen den partitionierten Teilen maximiert. Nachfolgend werden drei typische Splitkriterien näher erläutert. [1]
- Fehlerrate: Wenn p die Menge der einzelnen Instanzen (also einzelne Datenreihen in einem Datensatz) eines Datensatzes ist, welche zum dominierenden Wert der Zielvariable gehören, dann ist die Fehlerrate 1 - p. Die gesamte Fehlerrate einer Partitionierung bzw. Split eines Trainings Datensatzes mit einem Split-Kriterium errechnet sich mit dem gewichteten Durchschnitt der einzelnen Fehlerraten der einzelnen Partitionen. Das Gewicht einer Fehlerrate ist der Anteil der einzelnen Instanzen zum gesamten Datensatz. Es wird das Split-Kriterium mit der geringsten Fehlerrate gewählt. [1]
- Gini Index: Der Gini Index G(S) von einer Datenmenge S berechnet sich mit der nachfolgenden Gleichung mit der Verteilung der Werte der Zielvariablen p1 ... pk des Trainings Datensatzes. Der gesamte Gini Index für eine Partitionieren bzw. Split errechnet sich mit dem gewichteten Durchschnitt der einzelnen Gini Index Werte. Das Split-Kriterium mit dem geringsten Gini-Index wird gewählt. [1]
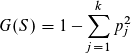
- Entropie: Die Entropie E(S) von einer Datenmenge S berechnet sich mit der nachfolgenden Gleichung. Die Verteilung der Werte von der Zielvariablen zum Trainingsdatensatz wird als p1 ... pk bezeichnet. Die gesamte Entropie für eine Partitionieren bzw. Split errechnet sich mit dem gewichteten Durchschnitt der einzelnen Entropie Werte. Das Split-Kriterium mit dem geringsten Entropie Wert wird gewählt. [1]
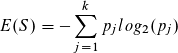
Stopp-Kriterien und Pruning
Wenn ein Decision Tree bis zum allerletzten Blatt erstellt wird bis alle Blätter jeweils nur noch Datenmengen eines Wertes der Zielvariablen enthalten, dann weist der Decision Tree eine Genauigkeit von 100% in Bezug auf den Trainingsdatensatz auf. Leider hat sich gezeigt, dass ein solcher Decision Tree sich schlecht auf neue, unvorhergesehene Daten verhält. Im Allgemeinen sind einfachere und weniger komplexe Decision Trees zu bevorzugen um ein Overfitting zu vermeiden. [3]
Mit einem Stopp-Kriterium (z. B. eine festgelegte Fehlerrate) lässt sich das wachsen des Decision Trees aufhalten. Leider gibt es keine Möglichkeit vorherzusagen an welchem Punkt der Decision Tree aufhören soll zu wachsen. Daher ist eine gängige Strategie bestimmte Knoten Teile zu entfernen oder zu konvertieren (Pruning). Eine Pruning-Strategie ist das Verwenden einer Kostenfunktion, welche beispielsweise die Fehlerrate sowie die Komplexität (Anzahl der Knoten und Informations-theoretische Prinzipien) des Decision Trees berücksichtigen. [1]
1. Aggarwal, C.: Data Mining: The textbook. Springer (Herausgeber) (2015)
2. Cleve, J., Lämmel, U.: Data Mining. Walter de Gruyter GmbH (Herausgeber) (2016)
3. Witten, I., Frank, E., Hall, M.: Data Mining. Morgan Kaufmann (Herausgeber) (2011)
Author: Yannick Kloss