Rechenbeispiel
Als Datengrundlage dient das Dataset auf github: https://github.com/gr8Adakron/naive-bayes-using-python/blob/master/tennis.csv
Die Tabelle enthält die normalen Attrbiute Outlook, Temperatur, Humidity und Windy. Play ist das Label Attribut, nach dem es zu klassifizieren gilt.
| Outlook | Temp. | Humidity | Windy | Play |
|---|---|---|---|---|
| sunny | hot | high | false | no |
| sunny | hot | high | true | no |
| overcast | hot | high | false | yes |
| rainy | mild | high | false | yes |
| rainy | cool | normal | false | yes |
| rainy | cool | normal | true | no |
| overcast | cool | normal | true | yes |
| sunny | mild | high | false | no |
| sunny | cool | normal | false | yes |
| rainy | mild | normal | false | yes |
| sunny | mild | normal | true | yes |
| overcast | mild | high | true | yes |
| overcast | hot | normal | false | yes |
| rainy | mild | high | true | no |
Der folgende Datensatz soll klassifiziert werden.
| Outlook | Temp. | Humidity | Windy | Play |
|---|---|---|---|---|
| sunny | hot | high | false | ? |
Wir suchen also die Wahrscheinlichkeiten für die Klassen yes und no unter der Bedingung der Instanzen.
Für die erste Instanz sieht dies so aus:
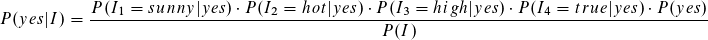
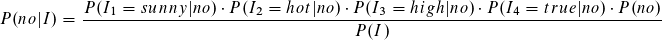
Fangen wir mit der Klasse yes und folgendem Term an.

Unter der Bedingung der Klasse yes (Anzahl 9) zählen wir 2 Instancen mit sunny. Somit beträgt die bedingte Wahrscheinlichkeit für den Term:
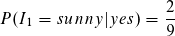
Wir verfahren analog mit den anderen Attributen:
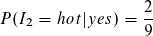

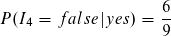
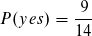
Nun können wir bereits den Likelihood für die Klasse yes ausrechnen bzw. fast den kompletten Term außer P(i).
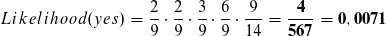
Wir verfahren analog zu der Klasse no,
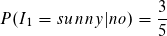
sowie mit den anderen Attributen und erhalten die Formel für den Likelihood.
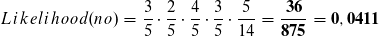
Der Likelihood für die Klasse no ist höher und die Instanz wird somit als no klassifiziert. Der Term P(I), die Wahrscheinlichkeit für die Instanz, ist uns unbekannt. Dennoch können wir die Wahrscheinlichkeit für die Klasse anhand der bereits errechneten Likelihoods bestimmen.
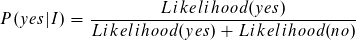
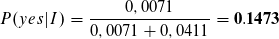
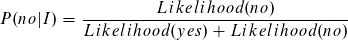
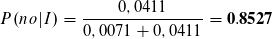
Zu 85% trifft die Klassifizierung zu no zu.
Author: Sven Schirmer